Examples
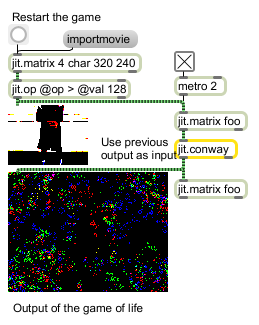
Conway's game of life (cellular automata)
The jit.conway object performs Conway's Game of Life on incoming 1- or 4-plane character matrices.
Devised by mathematician John Conway (1937-), the Game of Life treats the cells that comprise a matrix as either dead (0) or alive (non-0). The matrix is then modified according to the following rules:
If a live (non-0) cell has two or three neighbors, it remains alive. otherwise it dies (becomes 0).
If a dead cell has exactly three neighbors it becomes alive (255). otherwise it stays dead.
The jit.conway object works on 1- and 4-plane char data. It is usually used in a matrix feedback network so that multiple generations of the game can be calculated (see the help patch for details). The jit.conway object treats the incoming matrix as a torus space (i.e. the top wraps to the bottom and the left wraps to the right), so that cells can travel off one edge of the matrix and reappear on the opposite edge.
| Name | IOProc | Planelink | Typelink | Dimlink | Plane | Dim | Type |
| out | n/a | 1 | 1 | 1 | 1 | 1 | char |
| Name | Type | g/s | Description |
|---|---|---|---|
| birthmark | int | Defines whether newborn cells are set to 255 (off) or to the average of the contributing neighbor cells (on) (default = 0). | |
| deathmask | int | A mask setting whether a given number of live (non-0) neighbors will make a dead (0) cell come to life (default = 0 0 0 1 0 0 0 0 0). The first element in the list is the mask value for 0 live neighbors. | |
| lifemask | int | A mask setting whether a given number of live (non-0) neighbors will keep a live (non-0) cell alive (default = 0 0 1 1 0 0 0 0 0). The first element in the list is the mask value for 0 live neighbors. | |
| neighborhood | int | A mask for which neighbors around a cell are tallied to determine whether the cell changes state (default = 1 1 1 1 1 1 1 1). Ordering is upper-left, upper, upper-right, left, right, lower-left, lower, lower-right. |

| Name | Description |
|---|---|
| jit.linden | Lindenmayer string expansion (L-systems) |
| Tutorial 17: Feedback Using Named Matrices | Tutorial 17: Feedback Using Named Matrices |