Working with Transforms

In the previous article, we looked at using the coordinate system to position elements that we wanted to draw, including the difference between relative and absolute coordinates. However, we can also position elements by changing the coordinate system using transformations, including translation, rotation, and scaling. These transformations can make drawing much simpler, especially when drawing repeating elements.

Saving and Restoring State

Since these transformations modify the coordinate grid agaisnt which elements are drawn, it's useful to be able to save the current state of the grid so we can return to it later. The MGraphics functions save() and restore() let us save and restore the state of the drawing context so we can return to it later.

save() — Save the entire state of the drawing context

restore() — Restores the most recently saved state.

Calling save() pushes the state of the drawing context onto a stack. A drawing state consists of:

• The transformations that have been applied (i.e., translate, rotate and scale – see below).
• The current MGraphics state, including stroke and fill color, the line style, and font style.

You can call save() as many times as you like. Each time the restore() method is called, the last saved state is popped off the stack and all saved settings are restored.

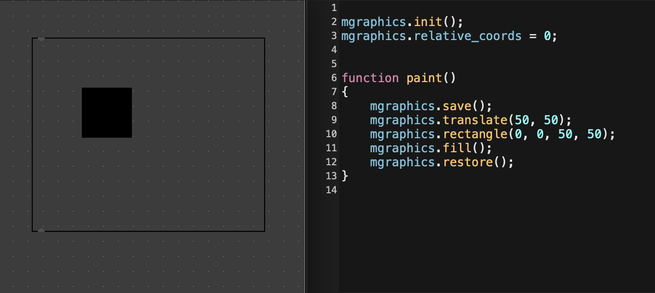
Translate

Calling translate() shifts the grid horizontally and vertically to a new origin.

mgraphics.init();
mgraphics.relative_coords = 0;

function paint()
{	
  mgraphics.save();
  mgraphics.translate(50, 50);
  mgraphics.rectangle(0, 0, 50, 50);
  mgraphics.fill();
  mgraphics.restore();
}

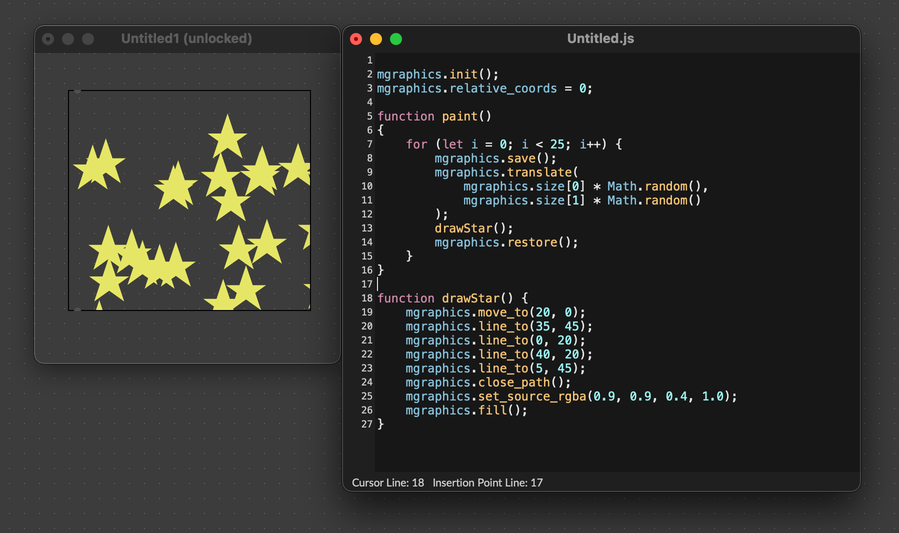
Translation can be useful for drawing a complex shape at a given position, without needing to modify the drawing code. For example, this code draws a five-pointed star at random points in the canvas.

mgraphics.init();
mgraphics.relative_coords = 0;

function paint()
{	
	for (let i = 0; i < 25; i++) {
		mgraphics.save();
		mgraphics.translate(
			mgraphics.size[0] * Math.random(),
			mgraphics.size[1] * Math.random()
		);
		drawStar();
		mgraphics.restore();
	}
}

function drawStar() {
	mgraphics.move_to(20, 0);
	mgraphics.line_to(35, 45);
	mgraphics.line_to(0, 20);
	mgraphics.line_to(40, 20);
	mgraphics.line_to(5, 45);
	mgraphics.close_path();
	mgraphics.set_source_rgba(0.9, 0.9, 0.4, 1.0);
	mgraphics.fill();
}

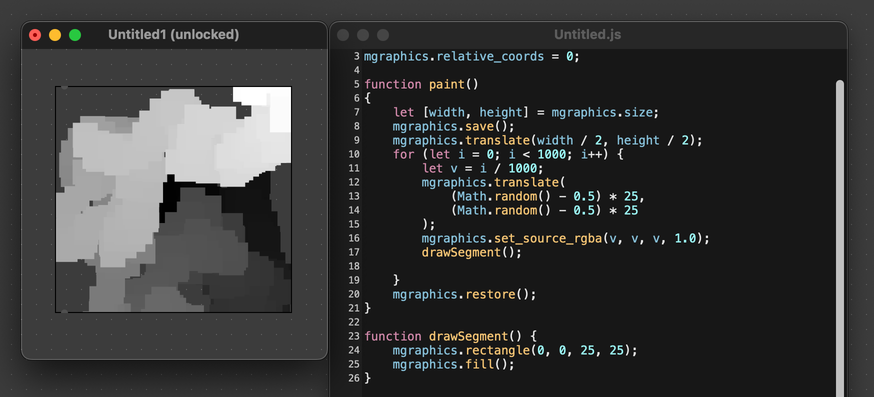
Like other transforms, translate is also useful for iterated drawing. For example, you could use the following code to draw a "snake" made of repeated segments.

mgraphics.init();
mgraphics.relative_coords = 0;

function paint()
{	
	let [width, height] = mgraphics.size;
	mgraphics.save();
	mgraphics.translate(width / 2, height / 2);
	for (let i = 0; i < 1000; i++) {
		let v = i / 1000;
		mgraphics.translate(
			(Math.random() - 0.5) * 25,
			(Math.random() - 0.5) * 25
		);
		mgraphics.set_source_rgba(v, v, v, 1.0);
		drawSegment();
		
	}
	mgraphics.restore();
}

function drawSegment() {
	mgraphics.rectangle(0, 0, 25, 25);
	mgraphics.fill();
}

Rotate

The rotate() function rotates the coordinate grid by some number of radians, with $2\pi$ radians corresponding to a full rotation. Rotations are about the origin of the coordinate system. Positive values rotate clockwise, while negative values rotate counterclockwise.

mgraphics.init();
mgraphics.relative_coords = 0;

function paint()
{	
	let [width, height] = mgraphics.size;
	for (let i = 0; i < 10; i++) {
		mgraphics.save();
		mgraphics.rotate(i * 0.75 / 10);
		mgraphics.rectangle(width / 2, height / 3, 45, 45);
		mgraphics.set_source_rgb(i / 10, i / 10, 1);
		mgraphics.fill();
		mgraphics.restore();
	}
}

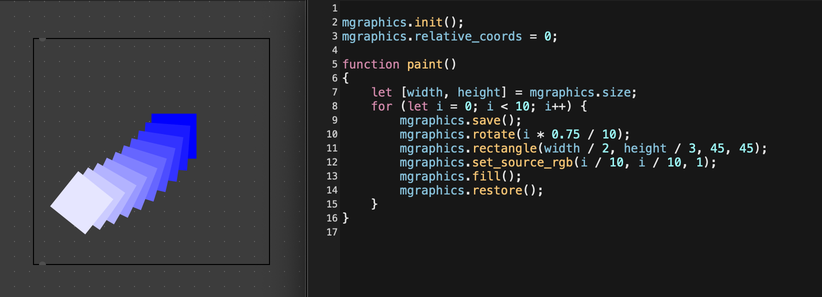
If you want to rotate the shape itself, you can first translate your path to the origin, perform your rotation, and then translate the shape back to the place where you want to draw it. For example, the following code would draw a rotated rectangle in the middle of the drawing context.

mgraphics.init();
mgraphics.relative_coords = 0;

let dim = 125;
function paint()
{	
	let [width, height] = mgraphics.size;
	
	for (let i = 0; i < 10; i++) {
		mgraphics.save();
		
		// Move to the position where you want to draw the shape
		mgraphics.translate(width / 4, height / 4);
		
		// Move the origin to the center of the shape
		mgraphics.translate(dim / 2, dim / 2);
		
		// Rotate
		mgraphics.rotate(i * 1.4 / 10);
		
		// Move back to the position where you want to draw the shape
		mgraphics.translate(-dim / 2, -dim / 2);
		
		mgraphics.rectangle(0, 0, dim, dim);
		mgraphics.set_source_rgb(i / 10, i / 10, 1 - i / 10);
		mgraphics.fill();
		mgraphics.restore();
	}
}

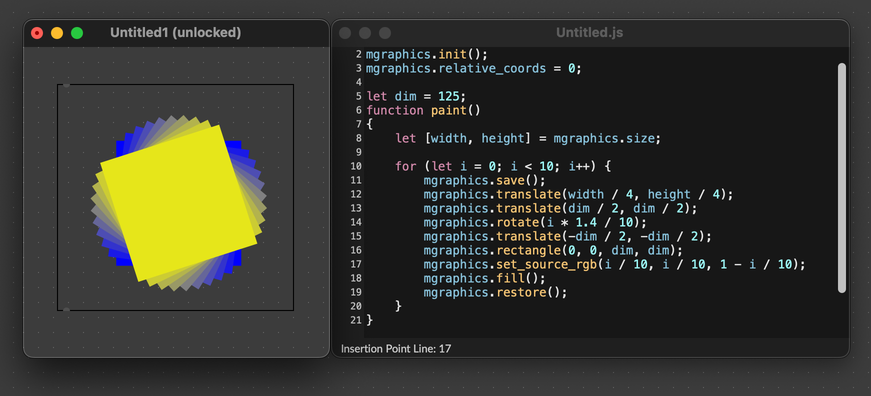
Scale

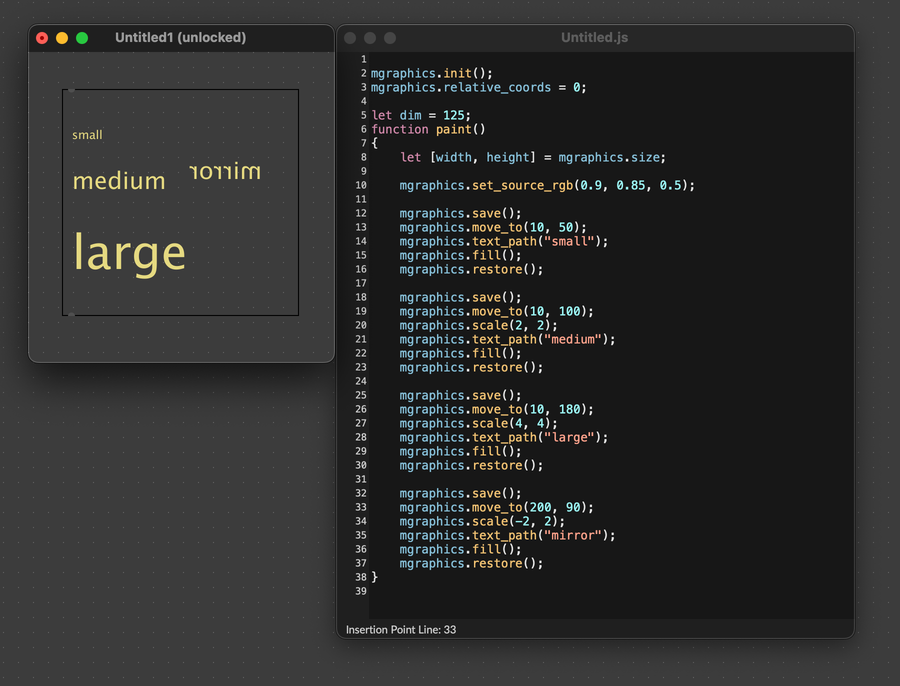
Last but not least, we have the scale() transformation. This stretches or shrinks the coordinate grid, changing the size of paths and images that we try to draw. You can change the scale in the X and Y direction independently. Values smaller than 1 will shrink the grid, while values larger than 1 will expand it. Negative values will invert the grid, mirroring about the X or Y axis.

mgraphics.init();
mgraphics.relative_coords = 0;

function paint()
{	
	let [width, height] = mgraphics.size;
	
	mgraphics.set_source_rgb(0.9, 0.85, 0.5);
	
	mgraphics.save();
	mgraphics.move_to(10, 50);
	mgraphics.text_path("small");
	mgraphics.fill();
	mgraphics.restore();
	
	mgraphics.save();
	mgraphics.move_to(10, 100);
	mgraphics.scale(2, 2);
	mgraphics.text_path("medium");
	mgraphics.fill();
	mgraphics.restore();
	
	mgraphics.save();
	mgraphics.move_to(10, 180);
	mgraphics.scale(4, 4);
	mgraphics.text_path("large");
	mgraphics.fill();
	mgraphics.restore();
	
	mgraphics.save();
	mgraphics.move_to(200, 90);
	mgraphics.scale(-2, 2);
	mgraphics.text_path("mirror");
	mgraphics.fill();
	mgraphics.restore();
}

Generic Transforms

It's also possible to apply a transform directly, combining translation, scaling, and rotation. For this, you can use the transform() function.

transform(xx: number, xy: number, yx: number, yy: number, x0: number, y0: number);

You can call the identity_matrix() function to reset the current transform, clearing any transformations that have already been applied.

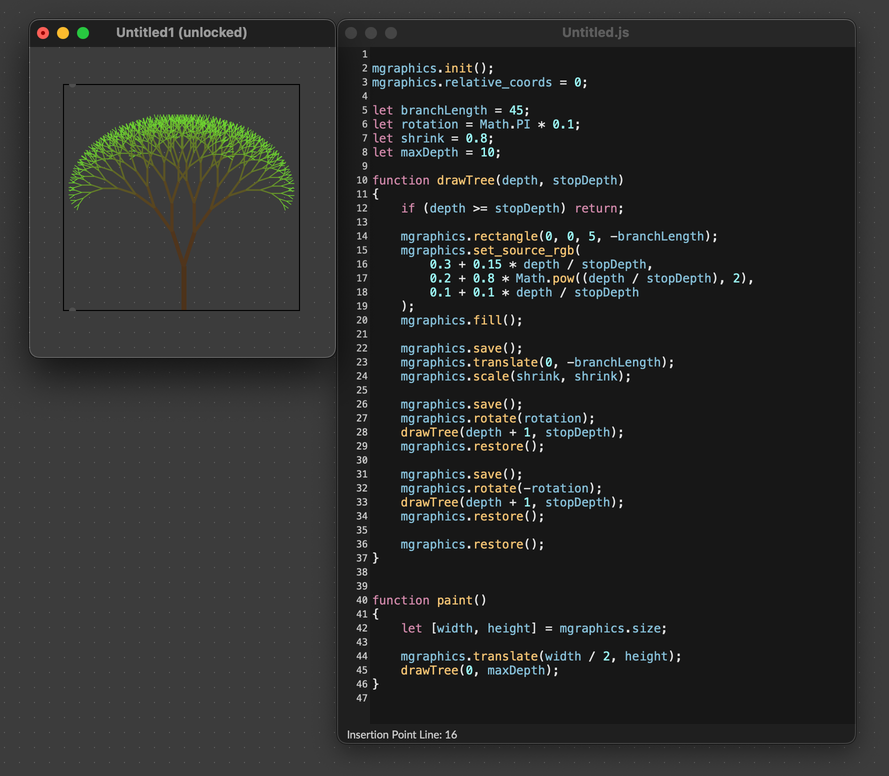
Combining Transforms

You can combine scale, rotate, and translate transformations to achieve complex drawing. The classic example is to use this method to draw a fractal "tree", where at each branch we apply a given translation, rotation, and scale before drawing the next branch. Lots of interesting fractal shapes can be drawn this way.

mgraphics.init();
mgraphics.relative_coords = 0;

let branchLength = 45;
let rotation = Math.PI * 0.1;
let shrink = 0.8;
let maxDepth = 10;

function drawTree(depth, stopDepth)
{
	if (depth >= stopDepth) return;
	
	mgraphics.rectangle(0, 0, 5, -branchLength);
	mgraphics.set_source_rgb(
		0.3 + 0.15 * depth / stopDepth,
		0.2 + 0.8 * Math.pow((depth / stopDepth), 2),
		0.1 + 0.1 * depth / stopDepth
	);
	mgraphics.fill();
	
	mgraphics.save();
	mgraphics.translate(0, -branchLength);
	mgraphics.scale(shrink, shrink);
	
	mgraphics.save();
	mgraphics.rotate(rotation);
	drawTree(depth + 1, stopDepth);
	mgraphics.restore();
	
	mgraphics.save();
	mgraphics.rotate(-rotation);
	drawTree(depth + 1, stopDepth);
	mgraphics.restore();
	
	mgraphics.restore();
}
	

function paint()
{	
	let [width, height] = mgraphics.size;
	
	mgraphics.translate(width / 2, height);
	drawTree(0, maxDepth);
}