Drawing contours

If you had a pencil and paper, and you had to draw a duck, what would your drawing look like? I had fun putting together a patch that takes a Jitter geomerty and draws some lines along the contours of the mesh.

Pencil and paper

Open the patch contours.maxpat.

Looking at the render, you can see that the mesh outlines have been drawn. But, how can we identify which portions of the mesh should be considered part of the outlines?

Give a look at the patch:

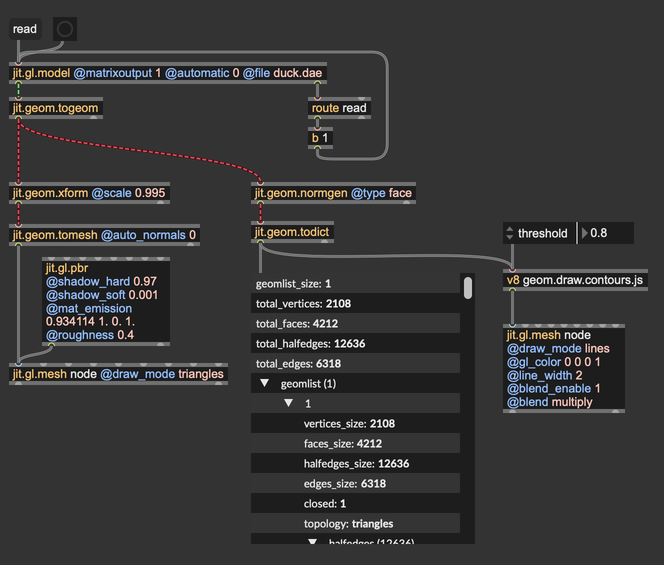
The first step consists in grabbing a mesh, turning it into a Jitter geometry, and computing face normals using jit.geom.normgen. They will come in handy later on.

Then, jit.geom.todict converts the Jitter geometry into a dictionary accessible by JavaScript.

Now, double-click on the v8 object v8 geom.draw.contours.js to give a look at the custom geometry script.

// Go through all the edges
edges.forEach(edge => {

  // An edge has one property, a list of the two half edge indexes
  let he0 = edge.halfedges[0];
  let he1 = edge.halfedges[1];

  // get the index of the faces divided by this edge
  let face0 = geom.halfedges[he0].face;
  let face1 = geom.halfedges[he1].face;

  // get their face normals
  let normal0 = geom.faces[face0].normal;
  let normal1 = geom.faces[face1].normal;

  // compute the cosine of the angle formed by the two faces
  let cosine = dot(normal0, normal1);

  // if the cosine is minor than threshold, draw the contour!
  if(cosine < threshold) {

    // Get the actual vertex structure from the geometry
    let v0 = geom.vertices[geom.halfedges[he0].from];
    let v1 = geom.vertices[geom.halfedges[he0].to];

    // Push the points into the list
    contourVertices.push(v0.point);
    contourVertices.push(v1.point);
  }
});

The core algorithm is pretty simple: only draw the edges that are formed when two faces meet at a steep angle. To do this, iterate over the edges of the mesh, checking the orientation (face normals) of the two faces divided by the edge. Then, if the cosine of the angle formed by the adjacent faces is less than than a user-defined threshold, draw a line connecting the endpoints of the edge.