Tutorial 24: Oscilloscope
There are times when seeing a picture of a signal is instructive. The scope~ object depicts the signal it receives, in the manner of an analog oscilloscope, as a graph of amplitude over time.
There are two problems scope~ must consider when plotting a graph of a signal in real time. First of all, in order for your eye to follow a time-varying signal, an excerpt of the signal must be captured and displayed for a certain period of time (long enough for you really to see it). Therefore, the graph must be displayed periodically, and will always lag a bit behind what you hear. Second, there aren't enough pixels on the screen for you to see a plot of every single sample (at least, not without the display being updated at blinding speed), so scope~ has to use a single pixel to summarize many samples.
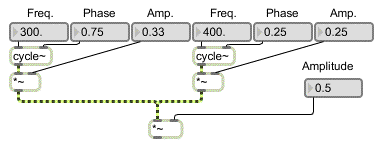
This tutorial shows how to get a useful display of a signal. The patch adds four cosine oscillators to create a variety of waveforms, and displays them in scope~. The frequency, phase, and amplitude of each sinusoid is set independently, and the over-all amplitude of the sum of the oscillators is scaled with an additional *~ object. The settings for each waveform are stored in a preset object.
Additive synthesis can be used to create a variety of complex waveforms
• Click on the first preset in the preset object.
When audio is turned on, the dspstate~ object sends the current sampling rate out its middle outlet. This is divided by the number of pixels per display buffer (the display buffer is where the display points are held before they're shown on the screen), and the result is the number of signal samples per display point (samples per pixel). This number is sent in the left inlet of scope~ to tell it how many samples to assign to each display pixel. The default number of pixels per display buffer is 128, so by this method each display will consist of exactly one second of signal. In other words, once per second scope~ displays the second that has just passed. We have stretched the scope~ (using its grow handle) to be 256 pixels wide -- twice its default width -- in order to provide a better view.
On the next page we will describe the different waveforms created by the oscillators.
• One by one, click on the different presets to see different waveforms displayed in the scope~. The first eight waves are at the sub-audio frequency of 1 Hz to allow you to see a single cycle of the waveform, so the signal is not sent to the dac~ until the ninth preset is recalled.
Preset 1. A 1 Hz cosine wave.
Preset 3. A 1 Hz cosine wave plus a 2 Hz cosine wave (i.e. octaves).
Preset 4. Four octaves: cosine waves of equal amplitude at 1, 2, 4, and 8 Hz.
Preset 5. A band-limited square wave. The four oscillators produce four sine waves with the correct frequencies and amplitudes to represent the first four partials of a square wave. (Although the amplitudes of the oscillators are only shown to two decimal places, they are actually stored in the preset with six decimal place precision.)
Preset 6. A band-limited sawtooth wave. The four oscillators produce four sine waves with the correct frequencies and amplitudes to represent the first four partials of a sawtooth wave.
Preset 7. A band-limited triangle wave. The four oscillators produce four sine waves with the correct frequencies and amplitudes to represent the first four partials of a triangle wave (which, it appears, is actually not very triangular without its upper partials).
Preset 8. This wave has the same frequencies and amplitudes as the band-limited square wave, but has arbitrarily chosen phase offsets for the four components. This shows what a profound effect the phase of components can have on the appearance of a waveform, even though its effect on the sound of a waveform is usually very slight.
Preset 9. A 32 Hz sinusoid plus a 36 Hz sinusoid (one-half cycle out of phase for the sake of the appearance in the scope~). The result is interference causing beating at the difference frequency of 4 Hz.
Preset 10. Combined sinusoids at 200, 201, and 204 Hz, producing beats at 1, 3, and 4 Hz.
Preset 11. Although the frequencies are all displayed as 200 Hz, they are actually 200, 200.25, 200.667, and 200.8. This produces a complicated interference pattern of six different sub-audio beat frequencies, a pattern which only repeats precisely every minute. We have set the number of samples per pixel much lower, so each display represents about 50 ms. This allows you to see about 10 wave cycles per display.
Preset 12. Octaves at 100, 200, and 400 Hz (with different phase offsets), plus one oscillator at 401 Hz creating beats at 1 Hz.
Preset 13. A cluster of equal-tempered semitones. The dissonance of these intervals is perhaps all the more pronounced when pure tones are used. Each display shows about 100 ms of sound.
Preset 14. A just-tuned dominant seventh chord; these are the 4th, 5th, 6th, and 7th harmonics of a common fundamental, so their sum has a periodicity of 100 Hz, two octaves below the chord itself.
Preset 15. Total phase cancellation. A sinusoid is added to a copy of itself 180° out of phase.
Preset 16. All oscillators off.
Summary
The scope~ object gives an oscilloscope view of a signal, graphing amplitude over time. Because scope~ needs to collect the samples before displaying them, and because the user needs a certain period of time to view the signal, the display always lags behind the signal by one display period. A display period (in seconds) is determined by the number of pixels per display buffer, times the number of samples per pixel, divided by the signal sampling rate. You can control those first two values by sending integer values in the inlets of scope~. The sampling rate of MSP can be obtained with the dspstate~ object.