Tutorial 7: Additive Synthesis
In the tutorial examples up to this point we have synthesized sound using basic waveforms. In the next few chapters we'll explore a few other well known synthesis techniques using sinusoidal waves. Most of these techniques are derived from pre-computer analog synthesis methods, but they are nevertheless instructive and useful.
A sine wave contains energy at a single frequency. Since complex tones, by definition, are composed of energy at several (or many) different frequencies, one obvious way to synthesize complex tones is to use multiple sine wave oscillators and add them together.

Four sinusoids added together to make a complex tone
Of course, you can add any waveforms together to produce a composite tone, but we'll stick with sine waves in this tutorial example. Synthesizing complex tones by adding sine waves is a somewhat tedious method, but it does give complete control over the amplitude and frequency of each component (partial) of the complex tone.
In the tutorial patch, we add together six cosine oscillators (cycle~ objects), with independent control over the frequency, amplitude, and phase of each one. In order to simplify the patch, we designed a subpatch called which allows us to specify the frequency of each partial as a ratio relative to a fundamental frequency.
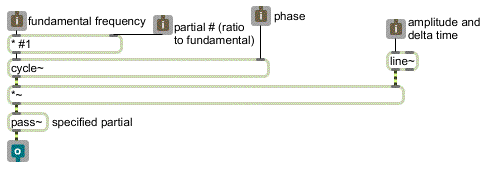
The contents of the subpatch partial~
For example, if we want a partial to have a frequency twice that of the fundamental we just type in as an argument (or send it in the second inlet). This way, if several subpatches are receiving their fundamental frequency value (in the left inlet) from the same source, their relative frequencies will stay the same even when the value of the fundamental frequency changes.
Of course, for the sound to be very interesting, the amplitudes of the partials must evolve with relative independence. Therefore, in the main patch, we control the amplitude of each partial with its own envelope generator.
In Tutorial 3 you saw how to create an amplitude envelope by sending a list of pairs of numbers to a line~ object, thus giving it a succession of target values and transition times. This idea of creating a control function from a series of line segments is useful in many contexts -- generating amplitude envelopes happens to be one particularly common usage -- and it is demonstrated in Tutorial 6, as well.
The function object is a great help in generating such line segment functions, because it allows you to draw in the shape that you want, as well as define the function's domain and range (the numerical value of its dimensions on the x and y axes). You can draw a function simply by clicking with the mouse where you want each breakpoint to appear. When function receives a , it sends a list of value-time pairs out its 2nd outlet. That list, when used as input to the line~ object, produces a changing signal that corresponds to the shape drawn.
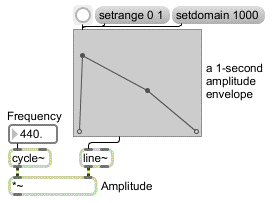
function is a graphic function generator for a control signal when used with line~
By the way, function is also useful for non-signal purposes in Max. It can be used as an interpolating lookup table. When it receives a number in its inlet, it considers that number to be an x value and it looks up the corresponding y value in the drawn function (interpolating between breakpoints as necessary) and sends it out the left outlet.
Even with only six partials, one can make a variety of timbres ranging from ‘realistic’ instrument- like tones to clearly artificial combinations of frequencies. The settings for a few different tones have been stored in a preset object, for you to try them out. A brief explanation of each tone is provided below.
• Click on the ezdac~ speaker icon to turn audio on. Click on the button to play a tone. Click on one of the stored presets in the preset object to change the settings, then click the button again to hear the new tone.
Preset 1. This tone is not really meant to emulate a real instrument. It's just a set of harmonically related partials, each one of which has a different amplitude envelope. Notice how the timbre of the tone changes slightly over the course of its duration as different partials come to the foreground. (If you can't really notice that change of timbre, try changing the note's duration to something longer, such as milliseconds, to hear the note evolve more slowly.)
Preset 2. This tone sounds rather like a church organ. The partials are all octaves of the fundamental, the attack is moderately fast but not percussive, and the amplitude of the tone does not diminish much over the course of the note. You can see and hear that the upper partials die away more quickly than the lower ones.
Preset 3. This tone consists of slightly mistuned harmonic partials. The attack is immediate and the amplitude decays rather rapidly after the initial attack, giving the note a percussive or plucked effect.
Preset 4. The amplitude envelopes for the partials in this tone are derived from an analysis of a trumpet note in the lower register. Of course, these are only six of the many partials present in a real trumpet sound.
Preset 5. The amplitude envelopes for the partials of this tone are derived from the same trumpet analysis. However, in this case, only the odd-numbered harmonics are used. This creates a tone more like a clarinet, because the cylindrical bore of a clarinet resonates the odd harmonics. Also, the longer duration of this note slows down the entire envelope, giving it a more characteristically clarinet-like attack.
Preset 6. This is a completely artificial tone. The lowest partial enters first, followed by the sixth partial a semitone higher. Eventually the remaining partials enter, with frequencies that lie between the first and sixth partial, creating a microtonal cluster. The beating effect is due to the interference between these waves of slightly different frequency.
Preset 7. In this case the partials are spaced a major second apart, and the amplitude of each partial rises and falls in such a way as to create a composite effect of an arpeggiated whole-tone cluster. Although this is clearly a whole-tone chord rather than a single tone, the gradual and overlapping attacks and decays cause the tones to fuse together fairly successfully.
Preset 8. In this tone the partials suggest a harmonic spectrum strongly enough that we still get a sense of a fundamental pitch, but they are sufficiently mistuned that they resemble the inharmonic spectrum of a bell. The percussive attack, rapid decay, and independently varying partials during the sustain portion of the note are also all characteristic of a struck metal bell.
Notice that when you are adding several signals together like this, their sum will often exceed the amplitude limits of the dac~ object, so the over-all amplitude must be scaled appropriately with a *~ object.
• Using these tones as starting points, you may want to try designing your own tones with this additive synthesis patch. Vary the tones by changing the fundamental frequency, partials, and duration of the preset tones. You can also change the envelopes by dragging on the breakpoints.
To draw a function in the function object:
• Click in the function object to create a new breakpoint. If you click and drag, the x and y coordinates of the point are shown in the upper portion of the object, and you can immediately move the breakpoint to the position you want.
• Similarly, you can click and drag on any existing breakpoint to move it.
• Shift-click on an existing point to delete it.
Although not demonstrated in this tutorial, it is also possible to create, move, and delete breakpoints in a function just by using Max messages. See the description of function in the Objects section of the manual for details.
The message , followed by a number, changes the scale of the x axis in the function without changing the shape of the envelope. When you change the number in the ‘Duration’ number box, it sends a message to the function.
Summary
Additive synthesis is the process of synthesizing new complex tones by adding tones together. Since pure sine tones have energy at only one frequency, they are the fundamental building blocks of additive synthesis, but of course any signals can be added together. The sum signal may need to by scaled by some constant signal value less than 1 in order to keep it from being clipped by the DAC.
In order for the timbre of a complex tone to remain the same when its pitch changes, each partial must maintain its relationship to the fundamental frequency. Stating the frequency of each partial in terms of a ratio to (i.e., a multiplier of) the fundamental frequency maintains the tone's spectrum even when the fundamental frequency changes.
In order for a complex tone to have an interesting timbre, the amplitude of the partials must change with a certain degree of independence. The function object allows you to draw control shapes such as amplitude envelopes, and when function receives a it describes that shape to a line~ object to generate a corresponding control signal.
See Also
| Name | Description |
|---|---|
| function | Graphical breakpoint function editor |