Tutorial 29: Flanging
So far, we have been delaying signals for a fixed amount of time using tapin~ and tapout~. You can change the delay time of any tap in the tapout~ object by sending a new number in the proper inlet; however, this will cause a discontinuity in the output signal at the instant when then new delay time is received, because tapout~ suddenly begins tapping a new location in the tapin~ buffer.
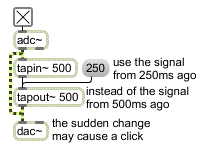
Changing the delay time creates a discontinuity in the output signal
On the other hand, it's possible to provide a new delay time to tapout~ using a continuous signal instead of a discrete Max message. We can use the line~ object to make a continuous transition between two delay times (just as we did to make continuous changes in amplitude in Tutorial 2).

Providing delay time in the form of a signal
Technical detail: Note that when the delay time is being changed by a continuous signal, tapout~ has to interpolate between the old delay time and the new delay time for every sample of output. Therefore, a tapout~ object has to do much more computation whenever a signal is connected to one of its inlets.
While this avoids the click that could be caused by a sudden discontinuity, it does mean that the pitch of the output signal will change while the delay time is being changed, emulating the Doppler effect
Technical detail: The Doppler effect occurs when a sound source is moving toward or away from the listener. The moving sound source is, to some extent, outrunning the wavefronts of the sound it is producing. That changes the frequency at which the listener receives the wavefronts, thus changing the perceived pitch. If the sound source is moving toward the listener, wavefronts arrive at the listener with a slightly greater frequency than they are actually being produced by the source. Conversely, if the sound source is moving away from the listener, the wavefronts arrive at the listener slightly less frequently than they are actually being produced. The classic case of Doppler effect is the sound of an ambulance siren. As the ambulance passes you, it changes from moving toward you (producing an increase in received frequency) to moving away from you (producing a decrease in received frequency). You perceive this as a swift drop in the perceived pitch of the siren.
A delayed signal emulates a reflection of the sound wave. As the delay time decreases, it is as if the (virtual) reflecting wall were moving toward you. The source of the delayed sound (the reflecting wall) is ‘moving toward you’, causing an increase in the received frequency of the sound. As the delay time increases, the reverse is true; the source of the delayed sound is effectively moving away from you. That is why, during the time when the delay time is actually changing, the perceived pitch of the output sound changes.
A delayed signal emulates a reflection of the sound wave. As the delay time decreases, it is as if the (virtual) reflecting wall were moving toward you. The source of the delayed sound (the reflecting wall) is ‘moving toward you’, causing an increase in the received frequency of the sound. As the delay time increases, the reverse is true; the source of the delayed sound is effectively moving away from you. That is why, during the time when the delay time is actually changing, the perceived pitch of the output sound changes.
A pitch shift due to Doppler effect is usually less disruptive than a click that's caused by discontinuity of amplitude. More importantly, the pitch variance that results from continuously varying the delay time can be used to create some interesting effects.
Since the delay time can be provided by any signal, one possibility is to use a time-varying signal like a low-frequency cosine wave to modulate the delay time. In the example below, a cycle~ object is used to vary the delay time.
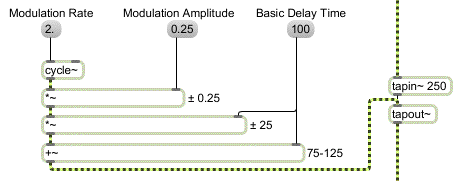
Modulating the delay time with a low-frequency oscillator
The output of cycle~ is multiplied by 0.25 to scale its amplitude. That signal is multiplied by the basic delay time of 100 ms, to create a signal with an amplitude ±25. When that signal is added to the basic delay time, the result is a signal that varies sinusoidally around the basic delay time of 100, going as low as 75 and as high as 125. This is used to express the delay time in milliseconds to the tapout~ object.
When a signal with a time-varying delay (especially a very short delay) is added together with the original undelayed signal, the result is a continually varying comb filter effect known as flanging. Flanging can create both subtle and extreme effects, depending on the rate and depth of the modulation.
This tutorial patch is very similar to that of the preceding chapter. The primary difference here is that the delay times of the two channels are being modulated by a cosine wave, as was described on the previous page. This patch gives you the opportunity to try a wide variety of flanging effects, just by modifying the different parameters: the wet/dry mix between delayed and undelayed signal, the left and right channel delay times, the rate and depth of the delay time modulation, and the amount of delayed signal that is fed back into the delay line of each channel.
• Send some sound into the audio input of the computer, and click on the buttons of the preset object to hear different effects. Using the example settings as starting points, experiment with different values for the various parameters. Notice that the modulation depth can also be controlled by the mod wheel of your synth, demonstrating how MIDI can be used for realtime control of audio processing parameters.
The different examples stored in the preset object are characterized below.
• 1. Simple thru of the audio input to the audio output. This is just to allow you to test the input and output.
• 2. The input signal is combined equally with delayed versions of itself, using short (mutually prime) delay times for each channel. The rate of modulation is set for 0.2 Hz (one sinusoid every 5 seconds), but the depth of modulation is initially 0. Use the mod wheel of your synth (or drag on the ‘Mod Wheel’ number box) to introduce some slow flanging.
• 3. The same as before, but now the modulation rate is 6 Hz. The modulation depth is set very low for a subtle vibrato effect, but you can increase it to obtain a decidedly un-subtle wide vibrato.
• 4. A faster vibrato, with greater depth, and with the delayed signal fed back into the delay line, creates a complex warbling flange effect.
• 5. The right channel is delayed a short time for a flange effect and the left channel is delayed a longer time for an echo effect. Both delay times change sinusoidally over a two second period, and each delayed signal is fed back into its own delay line (causing a ringing resonance in the right channel and repeated echoes in the left channel).
• 6. Both delay times are set long with considerable feedback to create repeated echoes. The rate (and pitch) of the echoes is changed up and down by a very slow modulating frequency -- one cycle every 10 seconds.
• 7. A similar effect, but modulated sinusoidally every 2 seconds.
• 8. Similar to example 5, but with flanging occurring at an audio rate of 55 Hz, and no original sound in the mix. The source sound is completely distorted, but the modulation rate gives the distortion its fundamental frequency.
Summary
You can provide a continuously varying delay time to tapout~ by sending a signal in its inlet. As the delay time varies, the pitch of the delayed sound shifts oppositely. You can use a repeating low frequency wave to modulate the delay time, achieving either subtle or extreme pitch-variation effects. When a sound with a varying delay time is mixed with the original undelayed sound, the result is a variable comb filtering effect known as flanging. The depth (strength) of the flanging effect depends primarily on the amplitude of the signal that is modulating the delay time.