What is a Matrix?

A matrix is a grid, with each location in the grid containing some information. For example, a chess board is a matrix in which every square contains a specific item of information: a particular chess piece, or the lack of a chess piece.

For the sake of this discussion, though, let's assume that the "information" at each location in a matrix is numeric data (numbers). Here's a matrix with a number at each grid location.

We'll call each horizontal line of data a row, and each vertical line of data a column. On roadmaps, or on chessboards, or in spreadsheet software, one often labels columns with letters and rows with numbers. That enables us to refer to any grid location on the map by referring to its column and its row. In spreadsheets, a grid location is called a cell. So, in the example above, the numeric value at cell C3 is 0.319.

The two pictures shown above are examples of matrices that have two dimensions, (horizontal) width and (vertical) height. In Jitter, a matrix can have any number of dimensions from 1 to 32. (A one-dimensional matrix is comparable to what programmers call an array. Max already has some objects that are good for storing arrays of numbers, such as table and multislider. There might be cases, though, when a one-dimensional matrix in Jitter would be more useful.) Although it's a bit harder to depict on paper, one could certainly imagine a matrix with three dimensions, as a cube having width, height, and depth. (For example, a matrix 3 cells wide by 3 cells high by 3 cells deep would have 3x3x3=27 cells total.)

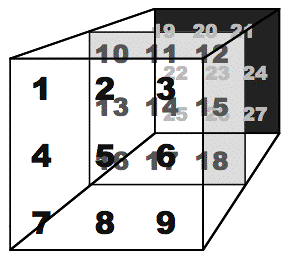
And although it challenges our visual imagination and our descriptive vocabulary, one can even have matrices of four or more dimensions. For this tutorial, however, we'll restrict ourselves to two-dimensional matrices.

A Video Screen is One Type of Matrix

A video screen is made up of tiny individual pixels (picture elements), each of which displays a specific color. On a computer monitor, the resolution of the screen is usually some size like 1024 pixels wide by 768 pixels high, or perhaps 800x600 or 640x480. On a television monitor (and in most conventional video images), the resolution of the screen is approximately 640x480, and on computers is typically treated as such. Notice that in all of these cases the so-called aspect ratio of width to height is 4:3. In the wider DV format, the aspect ratio is 3:2, and the image is generally 720x480 pixels. High-Definition Television (HDTV) specifies yet another aspect ratio—16:9. In these tutorials we'll usually work with an aspect ratio of 4:3, and most commonly with smaller-than-normal pixel dimensions 320x240 or even 160x120, just to save space in the Max patch.

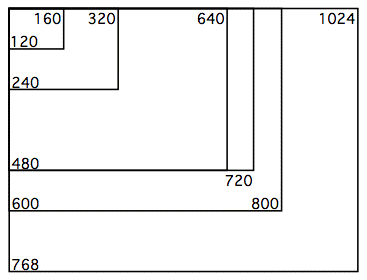
A single frame of standard video (i.e., a single video image at a given moment) is composed of 640x480=307,200 pixels. Each pixel displays a color. In order to represent the color of each pixel numerically, with enough variety to satisfy our eyes, we need a very large range of different possible color values.

There are many different ways to represent colors digitally. A standard way to describe the color of each pixel in computers is to break the color down into its three different color components —red, green, and blue ( a.k.a. RGB)—and an additional transparency/opacity component (known as the alpha channel). Most computer programs therefore store the color of a single pixel as four separate numbers, representing the alpha, red, green, and blue components (or channels). This four-channel color representation scheme is commonly called *ARGB or RGBA,*depending upon how the pixels are arranged in memory.

Jitter is no exception in this regard. In order for each cell of a matrix to represent one color pixel, each cell actually has to hold four numerical values (alpha, red, green, and blue), not just one. So, a matrix that stores the data for a frame of video will actually contain four values in each cell.

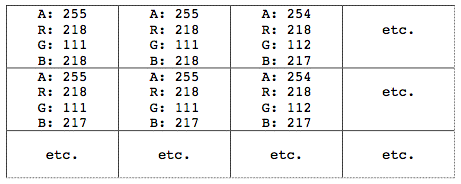
A frame of video is thus represented in Jitter as a two-dimensional matrix, with each cell representing a pixel of the frame, and each cell containing four values representing alpha, red, green, and blue on a scale from 0 to 255. In order to keep this concept of multiple-numbers-per-cell (which is essential for digital video) separate from the concept of dimensions in a matrix, Jitter introduces the idea of planes.

What is a Plane?

When allocating memory for the numbers in a matrix, Jitter needs to know the extent of each dimension—for example, 320x240—and also the number of values to be held in each cell. In order to keep track of the different values in a cell, Jitter uses the idea of each one existing on a separate plane. Each of the values in a cell exists on a particular plane, so we can think of a video frame as being a two-dimensional matrix of four interleaved planes of data.

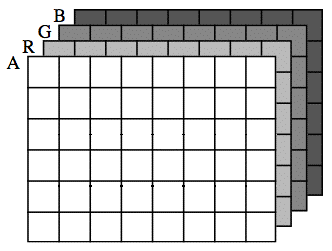
Using this conceptual framework, we can treat each plane (and thus each channel of the color information) individually when we need to. For example, if we want to increase the redness of an image, we can simply increase all the values in the red plane of the matrix, and leave the others unchanged.

The normal case for representing video in Jitter is to have a 2D matrix with four planes of data—alpha, red, green, and blue. The planes are numbered from 0 to 3, so the alpha channel is in plane 0, and the RGB channels are in planes 1, 2, and 3.

The Data in a Matrix

Computers have different internal formats for storing numbers. If we know the kind of number we will want to store in a particular place, we can save memory by allocating only as much memory space as we really need for each number. For example, if we are going to store Western alphabetic characters according to the ASCII standard of representation, we only need a range from 0 to 255, so we only need 8 bits of storage space to store each character (because 2⁸ = 256 different possible values). If we want to store a larger range of numbers, we might use 32 bits, which would give us integer numbers in a range from -2,147,483,648 to 2,147,483,647. To represent numbers with a decimal part, such as 3.1416, we use what is called a floating point binary system, in which some of the bits of a 32-bit or 64-bit number represent the mantissa of the value and other bits represent the exponent.

Much of the time when you are programming in Max (for example, if you're just working with MIDI data) you might not need to know how Max is storing the numbers. However, when you're programming digital audio in MSP it helps to be aware that MSP uses floating point numbers. (You will encounter math errors if you accidentally use integer storage when you mean to store decimal fractions.) In Jitter, too, it is very helpful to be aware of the different types of number storage the computer uses, to avoid possible math errors.

A Jitter matrix can store numbers as 64-bit floating-point (known to programmers as a double-precision float, or double), 32-bit floating point (known simply as float), 32-bit integers (known as long int, or just int), and 8-bit characters (known as char). Some jit objects store their numerical values in only one of these possible formats, so you will not have to specify the storage type. But other Jitter objects can store their values in various ways, so the storage type must be typed in as an argument in the object, using the words char, long, float32, or float64.