Synthesis Tutorial 2: Tremolo and Ring Modulation

Multiplying signals

In the previous tutorial we added sine tones together to make a complex tone. In this chapter we will see how a very different effect can be achieved by multiplying signals. Multiplying one wave by another - i.e., multiplying their instantaneous amplitudes, sample by sample - creates an effect known as ring modulation (or, more generally, amplitude modulation). ‘Modulation’ in this case simply means change; the amplitude of one waveform is changed continuously by the amplitude of another. In our example patch, we multiply two sinusoidal tones. Ring modulation (multiplication) can be performed with any signals, and in fact the most sonically interesting uses of ring modulation involve complex tones. However, we'll stick to sine tones in this example for the sake of simplicity, to allow you to hear clearly the effects of signal multiplication.

The tutorial patch contains two cycle~ objects, and the outlet of each one is connected to one of the inlets of a *~ object. However, the output of one of the cycle~ objects is first scaled by an additional *~ object, which provides control of the over-all amplitude of the result. (Without this, the over-all amplitude of the product of the two cycle~ objects would always be 1.)

Tremolo

When you first open the tutorial patch, a loadbang object initializes the frequency and amplitude of the oscillators. One oscillator is at an audio frequency of 1000 Hz. The other is at a sub-audio frequency of 0.1 Hz (one cycle every ten seconds). The 1000 Hz tone is the one we hear (this is termed the carrier oscillator), and it is modulated by the other wave (called the modulator) such that we hear the amplitude of the 1000 Hz tone dip to 0 whenever the 0.1 Hz cosine goes to 0. (Twice per cycle, meaning once every five seconds.)

• Click on the ezdac~ to turn audio on and raise the volume on the gain~ slider. You will hear the amplitude of the 1000 Hz tone rise and fall according to the cosine curve of the modulator, which completes one full cycle every ten seconds. (When the modulator is negative, it inverts the carrier, but we don't hear the difference, so the effect is of two equivalent dips in amplitude per modulation period.)

The amplitude is equal to the product of the two waves. Since the peak amplitude of the carrier is 1, the over-all amplitude is equal to the amplitude of the modulator.

• Drag on the number box labeled Amplitude to adjust the sound to a comfortable level. Click on the message box containing the number 1 to change the modulator rate.

With the modulator rate set at 1, you hear the amplitude dip to 0 two times per second. Such a periodic fluctuation in amplitude is known as tremolo. (Note that this is distinct from vibrato, a term usually used to describe a periodic fluctuation in pitch or frequency.) The perceived rate of tremolo is equal to two times the modulator rate, since the amplitude goes to 0 twice per cycle. As described on the previous page, ring modulation produces the sum and difference frequencies, so you're actually hearing the frequencies 1001 Hz and 999 Hz, and the 2 Hz beating due to the interference between those two frequencies.

• One at a time, message boxes containing 2 and 4. What tremolo rates do you hear? The sound is still like a single tone of fluctuating amplitude because the sum and difference tones are too close in frequency for you to separate them successfully, but can you calculate what frequencies you're actually hearing?

• Now try setting the rate of the modulator to 8 Hz, then 16 Hz.

In these cases the rate of tremolo borders on the audio range. We can no longer hear the tremolo as distinct fluctuations, and the tremolo just adds a unique sort of ‘roughness’ to the sound. The sum and difference frequencies are now far enough apart that they no longer fuse together in our perception as a single tone, but they still lie within what psychoacousticians call the critical band. Within this critical band we have trouble hearing the two separate tones as a pitch interval, presumably because they both affect the same region of our basilar membrane.

Sidebands

• Try setting the rate of the modulator to 32 Hz, then 50 Hz.

At a modulation rate of 32 Hz, you can hear the two tones as a pitch interval (approximately a minor second), but the sensation of roughness persists. With a modulation rate of 50 Hz, the sum and difference frequencies are 1050 Hz and 950 Hz - a pitch interval almost as great as a major second - and the roughness is mostly gone. You might also hear the tremolo rate itself, as a tone at 100 Hz.

You can see that this type of modulation produces new frequencies not present in the carrier and modulator tones. These additional frequencies, on either side of the carrier frequency, are often called sidebands.

• Listen to the remaining modulation rates.

At certain modulation rates, all the sidebands are aligned in a harmonic relationship. With a modulation rate of 200 Hz, for example, the tremolo rate is 400 Hz and the sum and difference frequencies are 800 Hz and 1200 Hz. Similarly, with a modulation rate of 500 Hz, the tremolo rate is 1000 Hz and the sum and difference frequencies are 500 Hz and 1500 Hz. In these cases, the sidebands fuse together more tightly as a single complex tone.

• Experiment with other carrier and modulator frequencies by typing other values into thenumber boxobjects. Note how different ratios of frequencies create different harmonic (or inharmonic) sidebands.

Technical detail: Multiplication of waveforms in the time domain is equivalent to convolution of waveforms in the frequency domain. One way to understand convolution is as the superimposition of one spectrum on every frequency of another spectrum. Given two spectra S1 and S2, each of which contains many different frequencies all at different amplitudes, make a copy of S1 at the location of every frequency in S2, with each copy scaled by the amplitude of that particular frequency of S2.Since a cosine wave has equal amplitude at both positive and negative frequencies, its spectrum contains energy (equally divided) at both f and -f. When convolved with another cosine wave, then, a scaled copy of (both the positive and negative frequency components of) the one wave is centered around both the positive and negative frequency components of the other.

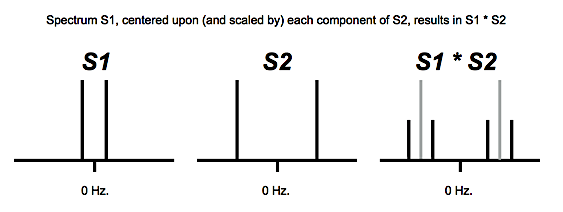
Technical detail: Multiplication of waveforms in the time domain is equivalent to convolution of waveforms in the frequency domain. One way to understand convolution is as the superimposition of one spectrum on every frequency of another spectrum. Given two spectra S1 and S2, each of which contains many different frequencies all at different amplitudes, make a copy of S1 at the location of every frequency in S2, with each copy scaled by the amplitude of that particular frequency of S2.Since a cosine wave has equal amplitude at both positive and negative frequencies, its spectrum contains energy (equally divided) at both f and -f. When convolved with another cosine wave, then, a scaled copy of (both the positive and negative frequency components of) the one wave is centered around both the positive and negative frequency components of the other.

Summary

Multiplication of two digital signals is comparable to the analog audio technique known as ring modulation. Ring modulation is a type of amplitude modulation - changing the amplitude of one tone (termed the carrier) with the amplitude of another tone (called the modulator). Multiplication of signals in the time domain is equivalent to convolution of spectra in the frequency domain.

Multiplying an audio signal by a sub-audio signal results in regular fluctuations of amplitude known as tremolo. Multiplication of signals creates sidebands - additional frequencies not present in the original tones. Multiplying two sinusoidal tones produces energy at the sum and difference of the two frequencies. This can create beating due to interference of waves with similar frequencies, or can create a fused complex tone when the frequencies are harmonically related. When two signals are multiplied, the output amplitude is determined by the product of the carrier and modulator amplitudes.