MSP Panning Tutorial 1: Simple panning

This tutorial references the patcher 01pMIDIPanning.maxpat

Panning for localization and distance effects

Loudness is one of the cues we use to tell us how far away a sound source is located. The relative loudness of a sound in each of our ears is a cue we use to tell us in what direction the sound is located. (Other cues for distance and location include inter-aural delay, ratio of direct to reflected sound, etc. For now we"ll only be considering loudness.)

When a sound is coming from a single speaker, we localize the source in the direction of that speaker. When the sound is equally balanced between two speakers, we localize the sound in a direction precisely between the speakers. As the balance between the two speakers varies from one to the other, we localize the sound in various directions between the two speakers.

The term panning refers to adjusting the relative loudness of a single sound coming from two (or more) speakers. On analog mixing consoles, the panning of an input channel to the two channels of the output is usually controlled by a single knob. In MIDI, panning is generally controlled by a single value from 0 to 127. In both cases, a single continuum is used to describe the balance between the two stereo channels, even though the precise amplitude of each channel at various intermediate points can be calculated in many different ways.

All other factors being equal, we assume that a softer sound is more distant than a louder sound, so the overall loudness effect created by the combined channels will give us an important distance cue. Thus, panning must be concerned not only with the proper balance to suggest direction of the sound source; it must also control the perceived loudness of the combined speakers to suggest distance.

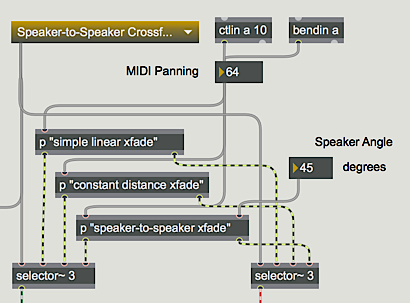
This tutorial demonstrates three ways of calculating panning, controllable by MIDI values 0 to 127. You can try out the three methods and decide which is most appropriate for a given situation in which you might want to control panning.

Patch for testing panning methods

To see how the sound is generated, double-click on the p’sound source’ subpatch to open its Patcher window.

Because of the gate~ object, nothing will be heard until a 1 is received in the inlet. At that time, the phasor~ generates a linear frequency glissando going from 2000 to 200 two times per second.

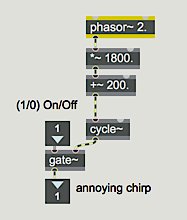
Close the subpatch window.

The output of this subpatch is sent to two *~ objects -- one for each output channel -- where its amplitude at each output channel will be scaled by one of the panning algorithms. You can choose the panning algorithm you want to try from the pop-up umenu at the top of the patch. This opens the inlet of the two selector~ objects to receive the control signals from the correct panning subpatch. It also opens an outlet of the gate object to allow control values into the desired subpatch. The panning is controlled by MIDI input from continuous controller No. 10 (designated for panning in MIDI).

In case your MIDI keyboard doesn"t send controller 10 easily, you can also use the pitch bend wheel to test the panning. (For that matter, you don"t need MIDI at all. You can just drag on the number box marked ‘MIDI panning’.)

Selection from the umenu opens input and output for one of the three panning subpatches

Linear crossfade

The most direct way to implement panning is to fade one channel linearly from 0 to 1 as the other channel fades linearly from 1 to 0. This is the easiest type of panning to calculate. We map the range of MIDI values 0 to 127 onto the amplitude range 0 to 1, and use that value as the amplitude for the right channel; the left channel is always set to 1 minus the amplitude of the left channel. The only hitch is that a MIDI pan value of 64 is supposed to mean equal balance between channels, but it is not precisely in the center of the range (⁶⁴/₁₂₇ ≠ 0.5). So we have to treat MIDI values 0 to 64 differently from values 65 to 127.

Double-click on the p‘simple linear xfade’ object to open its Patcher window.

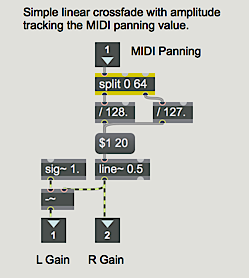
Linear crossfade using MIDI values 0 to 127 for control

Note that the output of line~ is sent directly out the right and subtracted from 1.0 before being sent out the left. This method seems perfectly logical since the sum of the two amplitudes is always 1. The problem is that the intensity of the sound is proportional to the sum of the squares of the amplitudes from each speaker. That is, two speakers playing an amplitude of 0.5 do not provide the same intensity (thus not the same perceived loudness) as one speaker playing an amplitude of 1. With the linear crossfade, then, the sound actually seems softer when panned to the middle than it does when panned to one side or the other.

Close the subpatch window. Choose ‘Simple Linear Crossfade’ from the umenu. Click on the ezdac~ to turn audio on, click on the toggle to start the ‘chirping’ sound, and use the ‘Amplitude’ number box to set the desired listening level. Move the pitch bend wheel of your MIDI keyboard to pan the sound slowly from one channel to the other. Listen to determine if the loudness of the sound seems to stay constant as you pan.

While this linear crossfade might be adequate in some situations, we may also want to try to find a way to maintain a constant intensity as we pan.

Equal distance crossfade

If we can maintain a constant intensity as we pan from one side to the other, this will give the impression that the sound source is maintaining a constant distance from the listener. Geometrically, this could only be true if the sound source were moving in an arc, with the listener at the center, so that the distance between the sound source and the listener was always equal to the radius of the arc.

It happens that we can simulate this condition by mapping one channel onto a quarter cycle of a cosine wave and the other channel onto a quarter cycle of a sine wave. Therefore, we"ll map the range of MIDI values 0 to 127 onto the range 0 to 0.25, and use the result as an angle for looking up the cosine and sine values.

Technical detail: As the sound source travels on a hypothetical arc from 0° to 90° (¹/₄ cycle around a circle with the listener at the center), the cosine of its angle goes from 1 to 0 and the sine of its angle goes from 0 to 1. At all points along the way, the square of the cosine plus the square of the sine equals 1. This trigonometric identity is analogous to what we are trying to achieve -- the sum of the squares of the amplitudes always equaling the same intensity -- so these values are a good way to obtain the relative amplitudes necessary to simulate a constant distance between sound source and listener.

Double-click on the p"constant distance xfade" object to open its Patcher window.

MIDI values 0 to 127 are mapped onto 1/4 cycle of cosine and sine functions

Once again we need to treat MIDI values greater than 64 differently from those less than or equal to 64, in order to retain 64 as the ‘center’ of the range. Once the MIDI value is mapped into the range 0 to 0.25, the result is used as a phase angle two cycle~ objects, one a cosine and the other (because of the additional phase offset of 0.75) a sine.

Close the subpatch window. Choose ‘Equal Distance Crossfade’ from the umenu. Listen to the sound while panning it slowly from one channel to the other.

Is the difference from the linear crossfade appreciable? Perhaps you don"t care whether the listener has the impression of movement in an arc when listening to the sound being panned. But the important point is that the equal distance method is preferable if only because it does not cause a noticeable dip in intensity when panning from one side to the other.

Technical detail: The MIDI specification gives a definition for panning asG_L = cos(π/2 * max(0, (P-1)/126))G_R = sin(π/2 * max(0, (P-1)/126))where G is the gain of the channel and P is the control 10 value. This is pretty much the same formula as used above, except the two extreme left positions (P=0 and P=1) are the same. Thus the effective pan is from 1 to 127 with 64 in the center.

Speaker-to-speaker crossfade

Given a standard stereo speaker placement -- with the two speakers in front of the listener at equal distances and angles -- if an actual sound source (say, a person playing a trumpet) moved in a straight line from one speaker to the other, the sound source would actually be closer to the listener when it's in the middle than it would be when it's at either speaker. So, to emulate a sound source moving in a straight line from speaker to speaker, we will need to calculate the amplitudes such that the intensity is proportional to the distance from the listener.

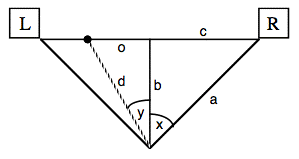
Technical detail: If we know the angle of the speakers (x and - x), we can use the cosine function to calculate distance a relative to distance b. Similarly we can use the tangent function to calculate distance c relative to b. The distance between the speakers is thus 2c, and as the MIDI pan value varies away from its center value of 64 it can be mapped as an offset (o) from the center ranging from -c to +c. Knowing b and o, we can use the Pythagorean theorem to obtain the distance (d). Armed with all of this information, we can finally calculate the gain for the two channels as a cos(y±x)/d.

Choose ‘Speaker-to-Speaker Crossfade’ from the umenu. Listen to the sound while panning it slowly from one channel to the other. You can try different speaker angles by changing the value in the ‘Speaker Angle’ number box. Choose a speaker angle best suited to your actual speaker positions.

This effect becomes more pronounced as the speaker angle increases. It is most effective with ‘normal’ speaker angles ranging from about 30° up to 45°, or even up to 60°. Below 30° the effect is too slight to be very useful, and above about 60° it"s too extreme to be realistic.

Double-click on the p"speaker-to-speaker xfade" object to open its Patcher window.

The trigonometric calculations described above are implemented in this subpatch. The straight ahead distance (b) is set at 1, and the other distances are calculated relative to it. The speaker angle -- specified in degrees by the user in the main patch -- is converted to a fraction of a cycle, and is eventually converted to radians (multiplied by 2π, or 6.2832) for the trigonometric operations. When the actual gain value is finally calculated, it is multiplied by a normalizing factor of 2/ (d+b) to avoid clipping. When the source reaches an angle greater than 90° from one speaker or the other, that speaker"s gain is set to 0.

To help get a better understanding of these calculations, move the pitch bend wheel and watch the values change in the subpatch. Then close the subpatch and watch the gain values change in the main Patcher window.

The signal gain values are displayed by an MSP user interface object called number~, which is explained in the next chapter.

Summary

MIDI controller No. 10 (or any other MIDI data) can be used to pan a signal between output channels. The relative amplitude of the two channels gives a localization cue for direction of the sound source. The overall intensity of the sound (which is proportional to the sum of the squares of the amplitudes) is a cue for perceived distance of the sound source.

Mapping the MIDI data to perform a linear crossfade of the amplitudes of the two channels is one method of panning, but it causes a drop in intensity when the sound is panned to the middle. Using the panning value to determine the angle of the sound source on an arc around the listener (mapped in a range from 0° to 90°), and setting the channel amplitudes proportional to the cosine and sine of that angle, keeps the intensity constant as the sound is panned.

When a sound moves past the listener in a straight line, it is loudest when it passes directly in front of the listener. To emulate straight line movement, one can calculate the relative distance of the sound source as it travels, and modify the amplitude of each channel (and the overall intensity) accordingly.