Introduction: What is Compression?
Dynamic compression is about level control. As an example, imagine recording a trumpet playing with a guitar. If you set the levels for the trumpet, the guitar will sound very quiet when played alone. If you set the levels for the guitar, the trumpet will be distorted when it comes in. So you ride gain, watching the trumpet player and turning the knob down when he's about to play. Compressors try to do this for you, adjusting the gain to keep the signal at a good strong level.
Any compression device has two parts: a circuit that measures the incoming signal, and a controlled amplifier that adjusts the gain of the output signal. The level measurement is connected to the gain control of the amplifier. This measurement is compared to a threshold setting to determine what the device will do. There are several options:
-
Most compressors used in recording reduce the gain of signals that are above the threshold. A compressor that completely flattens out all signal above the threshold is called a limiter.
-
Some compressors increase the gain of signals that are below the threshold, leaving signals above the threshold alone.
-
Compressors used in radio broadcasting boost soft signals and limit overly strong ones. These devices may be called comp/limiters or AGCs for automatic gain control.
-
Multiband compressors combine compression and graphic EQ, treating each frequency band independently. Multiband limiters are also available.
-
If the device reduces the gain of signals that measure below the threshold, it is expanding. The most common example of expansion is the noise gate, which has a very low threshold to shut off grunge in quiet moments.
-
In communications systems, signals are often compressed before they are sent and expanded upon reception. This helps reduce noise. The whole process is called companding.
This is all done to lesser or greater degrees based on a control that sets the amount of gain change. Gain change is expressed as a ratio. If this ratio is 2:1, a compressor would reduce a signal that is 6 dB above the threshold by half, until it is 3 dB above the threshold. If the ratio is 3:1, a +12 dB signal would be reduced to +4 dB.
The time it takes a compressor to respond to a change in signal level is important. It needs to be at least as long as a cycle of the lowest frequency coming in, which would be 1/30th of a second for a 30Hz tone. On the other hand, a rim shot is over in the same amount of time. A compressor fast enough to cover that would just pump up and down on the low tone. To handle this variety in material, compressors have controls for the speed of response. Usually there are two, attack time and release time, because musical sounds tend to start quickly and end slowly.
Threshold, ratio, attack time and release time are the vital parameters of a compressor. These determine what is heard and when. Most compressors have additional controls that set the details of measurement, input and output level, range of gain change and other options.
The tutorial patcher shows how a compression system is built. The signal coming in is split to a level measuring circuit and a gain control circuit. The measurement is done using the average~ object in rms mode. This is converted to dB for the gain calculations, which aren’t too complicated. In the subpatcher, the difference between the signal level and threshold is multiplied by a factor derived from the ratio. The result is converted back to absolute level and offset to create a gain correction value.
Back in the main patcher, a >~ object determines if the correction will be applied. This will switch abruptly from unity to corrected gain, a technique known as “hard knee” compression. (Most commercial units ease gently into gain reduction mode, providing “soft knees”.) The rampsmooth~ object slows down the gain changes. Note that the attack time of the compressor is set with a rampdown message. That’s because the gain is reduced when the compressor kicks in.
The final gain is multiplied by the input signal to provide the output.
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
20 log (A/B)
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
Decibels measure the ratio between sound levels. Sound levels vary tremendously, from about a watt down to a picowatt. This is a 1,000,000,000,000:1 ratio. With this wide a range, all you really need to know is the number of zeros in the ratio. A handy way of taming this number is to use logarithms. The formula for the dB relationship between two signal amplitudes is:
Usually B is some standard reference. With this formula, the dB value is positive if A is larger than the reference; if A is smaller, the value is negative. When the signals are the same, you get 0 dB. The reference in digital systems is almost always the full strength, so most signals are negative dB. In MSP a signal of 1.0. is 0 dB.Gain is a ratio between the signal coming in and the signal going out. This is usually in dB. If you chuck some common numbers into the dB formula, you find a doubling of the signal amplitude is a gain of 6 dB, and if it is increased tenfold, the change in dB is +20. Multiplying an MSP signal by 0.001 produces a reduction of 60 dB.Decibels are a useful way to measure signals because a change of 6 dB sounds about the same with soft sounds as with loud ones.
Measuring Signals
The level of a signal is tricky to measure. Since the waveform is a rapidly changing curve, there are various things to measure:
-
Peak amplitude is the highest sample value seen. (Or lowest- since samples are positive and negative, it's the absolute value we are interested in.)
-
Average amplitude is the average of the samples taken over some period of time.
-
RMS is the “root mean square” of absolute values of the sample values. That means square each sample, average those, then take the square root of the average. This math duplicates the action of an analog circuit that measures level.
The type of measurement made will also affect the action of a compression device. Usually limiters respond to peak levels, and compressors respond to averages.
Intermodulation Distortion
Intermodulation distortion, or IM, occurs when low frequency signals modulate the level of high frequency signals, or vice versa.
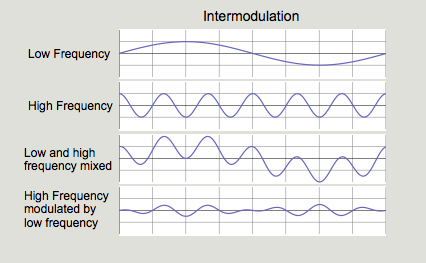
This is a pretty raw sound, as it includes components that are the sum of the two frequencies and the difference between the two frequencies. IM is quite common in electronic circuits and speakers, but it is usually a fraction of a percent of the original signal. Anything over 1% IM is noticeable, and 3% is downright annoying.