Basics Tutorial 4: Routing Signals

Introduction

In this tutorial we'll look at different ways to route MSP audio connections, as well as review sending messages remotely within Max with a focus on how this can be useful in signal network design. Along the way we'll learn about how gain can be expressed in decibels and how the phasor~ object works.

Remote signal connections: send~ and receive~

The patch cords that connect MSP objects look different from normal patch cords because they actually do something different. They describe the order of calculations in a signal network. These connected objects will be used to calculate a whole block of samples for the next portion of sound output by your computer.

Max objects can communicate remotely without patch cords by using the send and receive objects (and some similar objects such as value and pv). You can also use semicolons in message boxes to transmit values to receive objects by their name. You can transmit MSP signals remotely as well. Rather than using normal send and receive objects, however, two MSP objects exist specifically for remote transmission of signals: send~ and receive~.

The two objects send~ and receive~ work very similarly to send and receive, but are only for use with MSP signals. Max will allow you to connect normal patch cords to send~ and receive~, but only signals will get passed through send~ to the corresponding receive~.

Similar to how the names of send and receive can be shortened tos and r, the names of send~ and receive~ can be shortened tos~ and r~.

There are a few important differences between the Max objects send and receive and the MSP objects send~ and receive~.

1. A Max message can be sent to a receive object from several other objects besides send, such as float, forward, grab, if, int, and message; receive~ can receive a signal only from a send~ object that shares the same name.

2. If receive has no typed-in argument, it has an inlet for receiving set messages to set or change its name; receive~ also has an inlet for that purpose, but is nevertheless required to have a typed-in argument to give it an initial destination name.

3. The Max send object, once created, cannot change destinations (the Max forward object does this). The MSP send~ can change destinations with a set message.

Examples of each of these usages can be seen in the tutorial patch.

Routing a signal: gate~

The MSP object gate~ works very similarly to the Max gate object. Just as gate is used to direct messages to one of several destinations, or to shut the flow of messages off entirely, gate~ directs a signal to different places, or shuts it off from the rest of the signal network.

In the example patch, the gate~ objects are used to route signals to the left audio output, the right audio output, both, or neither, according to what number is received from the umenu object.

It is worth noting that changing the chosen outlet of a gate~ while an audio signal is playing through it can cause an audible click because the signal shifts abruptly from one outlet to another. To avoid this, you should generally design your patch in such a way that the gate~ object's outlet will only be changed when the audio signal going through it is at zero or when audio is off. (No such precaution was taken in this tutorial patch.)

The closed outlets of gate~ do not stop sending signals, they continue to send a signal with a constant value of 0. If the idea of a constant signal seems strange to you, think of it as 44,100 0s a second.

Wave interference

It's a fundamental physical fact that when we add together two sinusoidal waves with different frequencies we create interference between the two waves. Since they have different frequencies, they will usually not be exactly in phase with each other; at some times they will be sufficiently in phase that they add together constructively, but at other times they add together destructively, canceling each other out to some extent. They only arrive precisely in phase with each other at a rate equal to the difference in their frequencies. For example, a sinusoid at 1000 Hz and another at 1002 Hz come into phase exactly 2 times per second. In this case, they are sufficiently close in frequency that we don't hear them as two separate tones. Instead, we hear their recurring pattern of constructive and destructive interference as beats occurring at a sub-audio rate of 2 Hz, a rate known as the difference frequency or beat frequency. (Interestingly, we hear the two waves as a single tone with a sub-audio beat frequency of 2 Hz and an audio frequency of 1001 Hz.)

When the example patch is opened, a loadbang object sends initial frequency values to the two cycle~ objects in the patch, setting them to 1000 Hz and 1002 Hz; so we expect that these two tones sounded together will cause a beat frequency of 2 Hz. It also sends initial values to the umenu objects which in turn set the gate~ objects, directing one tone to the left audio output and one to the right audio output. A fourth value called Depth is also set. All of this is accomplished by using a message box to remotely set values picked up by Max receive objects in the patcher.

• In the tutorial patcher, click on ezdac~ to turn audio on, then use the slider marked Volume to adjust the loudness of the sound to a comfortable level. Note that the beats occur exactly twice per second. Try changing the frequency of Oscillator B to various other numbers close to 1000 (using the number box labeled frequency), and note the effect. As the difference frequency approaches an audio rate (say, in the range of 20-30 Hz) you can no longer distinguish individual beats, and the effect becomes more of a timbral change. Increase the difference still further, and you begin to hear two distinct frequencies.

• Philosophical tangent: It can be shown mathematically and empirically that when two sinusoidal tones are added, their interference pattern recurs at a rate equal to the difference in their frequencies. This apparently explains why we hear beats; the amplitude demonstrably varies at the difference rate. However, if you listen to this patch through headphones so that the two tones never have an opportunity to interfere mathematically, electrically, or in the air, you still hear the beats! This phenomenon, known as binaural beating is caused by ‘interference’ occurring in the nervous system. Although such interference is of a very different physical nature than the interference of sound waves in the air, we experience it as similar. An experiment like this demonstrates that our auditory system actively shapes the world we hear.

Amplitude and relative amplitude

The slider marked ‘Volume’ has been set to have a range of 101 values, from 0 to 100, which makes it easy to convert its output to a float ranging from 0 to 1 just by dividing by 100. (The decimal point in argument typed into the / object ensures a float division.)

The *~ objects use the specified amplitude value to scale the audio signal before it goes to the ezdac~. If both oscillators get sent to the same inlet of ezdac~, their combined amplitude will be 2. Therefore, it is prudent to keep the amplitude scaling factor at or below 0.5. For that reason, the amplitude value which the user thinks of as being between 0 and 1 is actually kept between 0 and 0.5 by the *0.5 object below the slider.

Because of the wide range of possible audible amplitudes, it may be more meaningful in some cases to display volume numerically in terms of the logarithmic scale of decibels (dB), rather than in terms of absolute amplitude. The decibel scale refers to relative amplitude, i.e. the amplitude of a signal relative to some reference amplitude. The formula for calculating amplitude in decibels is:

dB = 20(log10(A/Aref))

where A is the amplitude being measured and Aref is a fixed reference amplitude.

The AtodB object uses a reference amplitude of 1 in the formula shown above, and converts the amplitude to dB. If you turn off the audio (for safety) and raise the slider to its maximum value (ensuring an output of 1), you will see the decibel output of the AtodB object read 0 (i.e. unity gain). Each halving of the amplitude in the slider is approximately equal to a 6 dB reduction in decibels.

Constant signal value: sig~

Most signal networks require some changing values (such as an amplitude envelope to vary the amplitude over time) and some constant values (such as a frequency value to keep an oscillator at a steady pitch). In general, one provides a constant value to an MSP object in the form of a float message, as we have done in these examples when sending a frequency in the left inlet of a cycle~ object.

However, there are some cases when one wants to combine both constant and changing values in the same inlet of an MSP object. Inlets that accept either a float or a signal (such as the left inlet of cycle~) do not successfully combine the two. In general, MSP objects will ignore a floating-point value in deference to a signal input. As a result, it's necessary to have an object that outputs a constant value as a signal if you need to combine a fixed and changing value in an MSP signal chain.

One way to combine a numerical Max message (an int or a float) with a signal is to convert the number into a steady signal with the sig~ object. The output of sig~ is a signal with a constant value, determined by the number received in its inlet.

In the example patch, Oscillator B combines a constant frequency (supplied as a float to sig~) with a varying frequency offset (signal values coming in from a receive~ object called FreqB+). The sum of these signals will be the frequency of the oscillator at any given instant.

Changing the phase of a waveform: phasor~

For the most part, the phase offset of an isolated audio wave doesn't have a substantial effect perceptually. For example, a sine wave in the audio range sounds exactly like a cosine wave, even though there is a theoretical phase difference of a quarter cycle. For that reason, we have not been concerned with the rightmost phase inlet of the cycle~ object until now.

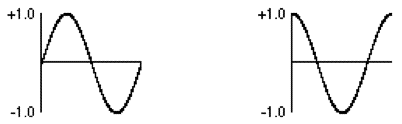
However, there are some very useful reasons to control the phase offset of a wave. For example, by leaving the frequency of cycle~ at 0, and continuously increasing its phase offset, you can change its instantaneous value (just as if it had a positive frequency). The phase offset of a sinusoid is usually referred to in degrees (a full cycle is 360°) or radians (a full cycle is 2*π radians in length). In the cycle~ object, phase is referred to in wave cycles; so an offset of π radians is 1/2 of a cycle, or 0.5. In other words, as the phase varies from 0 to 2π radians, it varies from 0 to 1 wave cycles. This way of describing the phase is handy since it allows us to use the common signal range from 0 to 1.

So, if we vary the phase offset of a stationary (0 Hz) cycle~ object continuously from 0 to 1 over the course of one second, the resulting output is a cosine wave with a frequency of 1 Hz.

The phasor~ object is a very useful MSP signal generator that simply outputs a ramp from 0 to 1 at a given frequency. As with the cycle~ object, it's frequency can be set by an argument to the object, a floating-point value in its left inlet, or a signal. Later in our tutorial, we'll hear what it sounds like (it's a sawtooth wave, and not an especially pleasant one), but for now let's use it for changing the phase (hence phasor~ of the cycle~ object in the lower-left of the tutorial patcher.

• Click on the message box above the line~ objects in the lower-left portion of the tutorial patch. You should hear one of the sine waves begin to slowly drop and rise in pitch, causing the beating between the two sines connected to the audio output to change over time.

The cycle~ in the bottom-left of the patcher is modulating the cycle~ object in the upper-right by adding a value to its current (constant) frequency, set by the sig~ object.

Receiving a different signal

The remaining portion of the tutorial patch exists simply to demonstrate the use of the set message to the receive~ object. This is another way to alter the signal flow in a network. As with the send~ object, you can change the name of the receive~ object with a set message, instructing it to get its input from a different send~ object (or objects).

• Click on the message box containing set sawtooth. Both of the connected receive~ objects now get their signal from the phasor~ object in the lower-right corner of the window. Click on the message boxes containing set outL and set outR messages to receive the sinusoidal tones once again. With the sawtooth destination selected, change the frequency of the phasor~ in the lower-right of the patcher. Notice that when set to an audible frequency, the ramp of the phasor~ object causes it to sound like an oscillator rich in harmonics. This is a sawtooth wave, a common waveform used in synthesizer design. Because the phasor~ object only ramps from 0 to 1 (and not -1 to 1), using a phasor~ as an audio source isn't the best way to get this sound: the MSP saw~ wave will do the trick instead.

Summary

It is possible to make signal connections without patch cords by using the MSP objects send~ and receive~, which are similar to the Max objects send and receive. The set message can be used to change the name of a send~ or receive~ object, thus switching how signals are routed. Signal flow can be routed to different destinations within a patcher, or shut off entirely, using the gate~ object, which is the MSP equivalent of the Max object gate.

The cycle~ object can be used not only for periodic audio waves, but also for sub-audio control functions: you can read through the waveform of a cycle~ object at any rate you wish by keeping its frequency at 0 Hz and changing its phase continuously from 0 to 1. The phasor~ object is appropriate for changing the phase of a cycle~ waveform in this way; you could also use a line~ object to create a ramp that goes through the object's wavetable.

The sig~ object converts a number to a constant signal; it receives a number in its inlet and sends out a signal of that value. This is useful for combining constant values with varying signals. Mixing together tones with slightly different frequencies creates interference between waves, which can create beats and other timbral effects.

See Also

• gate~ - Route a signal to one of several outlets

• receive~ - Receive signals without patch cords

• send~ - Transmit signals without patch cords

• sig~ - Constant signal of a number

• phasor~ - Sawtooth wave generator